1、查找的基本概念
查找表: 是由同一类型的数据元素(或记录)构成的集合。
关键字:是数据元素中某个数据项的值,又称为键值。主关键字、次关键字
查找:就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素。
静态查找表:只作查找操作的查找表。
动态查找表:在查找过程中同时插入查找表中不存在的数据元素,或者从查找表中删除已经存在的某个数据元素。
2、查找算法
2.1 顺序表查找
线性查找,逐个比较查找,是最基本的查找技术。时间复杂度: O(n)
2.2 有序表查找
(1) 折半查找:二分查找,时间复杂度:O(logn)
(2) 插值查找:时间复杂度:O(logn),适用于表长较长,并且关键字分布均匀的查找表。
(3) 斐波那契查找:时间复杂度:O(logn)
2.3 动态查找表
二叉排序树、平衡二叉树(AVL树)、B树
2.4 哈希表查找
散列(哈希)hash技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。
哈希函数:对应关系f
哈希表: 采用哈希函数记录关键字的这一段连续的存储空间
哈希函数的构造方法:直接定址法、数字分析法、平方取中法、折叠法、除留取余法、随机数法
处理散列冲突的方法:开放定址法、再散列函数法、链地址法。
3、各种查找算法的C实现
#include <stdio.h>
#include <stdlib.h>
// 1.顺序查找
// 顺序查找,a为数组,n为查找的数组长度,key为要查找的关键字
// 查找成功,返回数组索引;查找不成功,返回-1。
int Sequential_Search(int *a, int n, int key)
{
int i;
for (i = 0; i < n; i++)
{
if (key == a[i])
{
return i;
}
}
return -1;
}
// 2.带哨兵的顺序查找
int Sequential_Search2(int *a, int n, int key)
{
int i;
a[0] = key; // 在数组末尾设置哨兵
i = n;
while (a[i] != key)
{
i--;
}
return i; // 返回0说明查找失败
}
// 3.折半查找(二分查找)
int Binary_Search(int *a, int n, int key)
{
int low, high, mid;
low = 1;
high = n;
while (low <= high)
{
mid = (low+high)/2;
// mid = low + (high-low)*(key-a[low])/(a[high] - a[low]); //插值查找法
if (key < a[mid])
{
high = mid-1;
}
else if (key > a[mid])
{
low = mid+1;
}
else
return mid;
}
return 0;
}
const int F[13] = {0,1,1,2,3,5,8,13,21,34,55,89,144};
/* 4.斐波那契查找 */
int Fibonacci_Search(int *a, int n, int key)
{
int low, high, mid, i, k;
low = 1;
high =n;
k = 0;
while(n > F[k]-1)
k++;
for (i=n; i < F[k]-1;i++)
{
a[i] = a[n];
}
while (low <= high)
{
mid = low+F[k-1]-1;
if (key < a[mid])
{
high = mid - 1;
k = k-1;
}
else if (key > a[mid])
{
low = mid + 1;
k= k-2;
}
else
{
if (mid<=n)
{
return mid;
}
else
{
return n;
}
}
}
return 0;
}
// 5.二叉排序树
typedef struct BiTNode
{
int data;
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
//递归查找二叉排序树中是否存在Key
//若查找成功,则指针p指向该数据元素结点,并返回TRUE,否则指针p指向查找路径上
//访问的最后一个结点并返回FALSE
int SearchBST(BiTree T, int key, BiTree f, BiTree *p)
{
if (!T)
{
*p = T;
return -1;
}
else if (key == T->data)
{
*p = T;
return 0;
}
else if (key < T->data)
{
return SearchBST(T->lchild, key, T, p);
}
else
return SearchBST(T->rchild, key, T, p);
}
// 二叉排序树的插入操作
int InsertBST(BiTree *T, int key)
{
BiTree p, s;
if (!SearchBST(*T, key, NULL, &p)) // 查找不成功才插入
{
s = (BiTree) malloc(sizeof(BiTNode));
s->data = key;
s->lchild = s->rchild = NULL;
if (!p)
{
*T = s; // 插入s为新的根结点
}
else if (key < p->data)
{
p->lchild = s; // 插入s为左孩子
}
else
{
p->rchild = s;// 插入s为右孩子
}
return 0;
}
else
return -1;
}
int Delete(BiTree *p)
{
BiTree q, s;
if ((*p)->rchild == NULL)
{
q = *p;
*p = (*p)->lchild;
free(q);
}
else if ((*p)->lchild == NULL)
{
q = *p;
*p = (*p)->rchild;
free(q);
}
else
{
q = *p;
s = (*p)->lchild;
while (s->rchild)
{
q = s;
s = s->rchild;
}
(*p)->data = s->data;
if (q!=*p)
{
q->rchild = s->lchild;
}
else
q->lchild = s->lchild;
free(s);
}
return 0;
}
//二叉排序树的删除操作
int DeleteBST(BiTree *T, int key)
{
if (!*T) //空树
{
return -1;
}
else
{
if (key == (*T)->data) // 找到关键字为key的数据元素
{
return Delete(T);
}
else if (key < (*T)->data)
{
return DeleteBST(&(*T)->lchild, key);
}
else
return DeleteBST(&(*T)->rchild, key);
}
}
// 6.散列表查找
#define SUCCESS (1)
#define UNSUCCESS (0)
#define HASHSIZE (12)
#define NULLKEY (-32768)
typedef struct
{
int *elem;
int count;
} HashTable;
int m = 0; // 散列表表长,全局变量
int InitHashTable(HashTable *H)
{
int i;
m = HASHSIZE;
H->count = m;
H->elem = (int*) malloc(m*sizeof(int));
for (i = 0; i < m; i++)
{
H->elem[i] = NULLKEY;
}
return 0;
}
int Hash(int key)
{
return key % m; // 除留取余法
}
void InsertHash(HashTable *H, int key)
{
int addr = Hash(key);
while (H->elem[addr] != NULLKEY)
{
addr = (addr+1) % m;
}
H->elem[addr] = key;
}
// 散列表查找关键字
int SearchHash(HashTable H, int key, int *addr)
{
*addr = Hash(key);
while (H.elem[*addr] != key)
{
*addr = (*addr +1) % m;
if (H.elem[*addr] == NULLKEY || *addr == Hash(key))
{
return UNSUCCESS;
}
}
return SUCCESS;
}
int main(int argc, char* argv[])
{
int index = 0;
int i = 0;
int addr = 0;
int array[10] = {5, 4, 8, 10, 30, 40, 50, 60, 70, 80};
int a[10] = {62,88,85,47,35,73,51,99,37,93};
BiTree T = NULL;
HashTable H = {0};
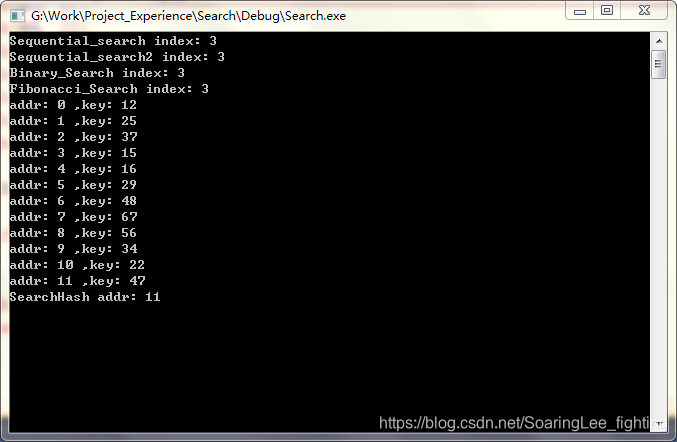
index = Sequential_Search(array, 10, 10);
printf("Sequential_search index: %d\n", index);
index = Sequential_Search2(array, 10, 10);
printf("Sequential_search2 index: %d\n", index);
index = Binary_Search(array, 10, 10);
printf("Binary_Search index: %d\n", index);
index = Fibonacci_Search(array, 10, 10);
printf("Fibonacci_Search index: %d\n", index);
for (i=0;i<10;i++)
{
InsertBST(&T, a[i]);
}
InitHashTable(&H);
InsertHash(&H, 12);
InsertHash(&H, 67);
InsertHash(&H, 56);
InsertHash(&H, 16);
InsertHash(&H, 25);
InsertHash(&H, 37);
InsertHash(&H, 22);
InsertHash(&H, 29);
InsertHash(&H, 15);
InsertHash(&H, 47);
InsertHash(&H, 48);
InsertHash(&H, 34);
for (i = 0; i < H.count; i++)
{
printf("addr: %d ,key: %d \n", i, H.elem[i]);
}
SearchHash(H, 47, &addr);
printf("SearchHash addr: %d\n", addr);
return 0;
}
THE END!
本博文只能阅读,谢绝转载,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 2963033731@qq.com


